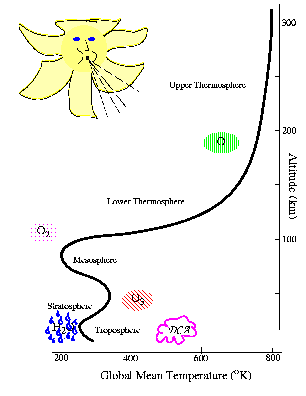
 The GSWM uses several heat forcing models. The figure
illustrates the location and mechanism of each major source of
thermal excitation available in the GSWM.
The GSWM uses several heat forcing models. The figure
illustrates the location and mechanism of each major source of
thermal excitation available in the GSWM.

Return to GSWM page/
Model Features/
Backgrounds/
Forcing/
Dissipation/
Description of Output/
Plots of the Background Atmosphere/
The FORTRAN model currently runs on NCAR's Cray J90 computer, and provides an ASCII format output file.
Back to Top of Model page.
These empirically-based mean background winds introduce significant asymmetries about the equator in both amplitude and phase in the solstice months.
Contour plots of the backgrounds that show the values of zonal mean temperature and zonal mean zonal winds for standard runs are available for each month from this web site. Other wind backgrounds commonly used for experimentation include composite wind fields which use measurements from the UARS HRDI instrument within a range of altitudes, mesospheric winds calculated by Portnyagin and Solov'eva (1992), pure geostrophic winds, and zero background winds.
Background ozone concentrations can also be chosen for each experiment. The standard configuration uses 7 year-averaged measurements from the HALOE instrument on the UARS satellite, enhanced with MLS measurements above about 50km. Other ozone backgrounds available come from the CIRA database, CLAES, and MLS. Plots of HALOE/MLS ozone used for standard model output are available here.
Back to Top of Model page.
 The GSWM uses several heat forcing models. The figure
illustrates the location and mechanism of each major source of
thermal excitation available in the GSWM.
The GSWM uses several heat forcing models. The figure
illustrates the location and mechanism of each major source of
thermal excitation available in the GSWM.
In the standard configuration, the tropospheric IR heat forcing models (blue raindrops) are based on Groves (1982), and are available for 4 months (January, April, July, October), representing 4 seasons of the year. All standard model output is therefore restricted to these months.
The standard model uses latitude and altitude-dependent ozone concentrations to calculate ozone (UV) forcing (red striped ellipse) in the stratosphere.
Latent heating models (low pink cloud)(Forbes and Groves, 1987; Williams and Avery, 1996; Hong and Wang 1980) that simulate the transport of energy by meterological systems are a more significant source of forcing for non-migrating tides, and are not used in the standard migrating tide model. However, these models may be combined with the ozone (UV) and water vapor (IR) forcing models for migrating tides, as well.
Finally, a simplified Hough (1,1) tropospheric driver may be used for
experiments that only approximate combined forcing to the first order.
Back to Top of Model page.
Tidal amplitudes generally increase with altitude as the density of the atmosphere decreases, however damping effects also become strong at higher altitudes. Gravity waves deposit momentum in the mesosphere and lower thermosphere as they break, which dominates the the tidal flow and "drags" it to the phase velocity of the gravity waves. This effect cancels the propagation of the diurnal (24 hour) migrating tide at the mesosphere (making it "effervescent", or "trapped"), so that diurnal winds are much weaker in the lower thermosphere.
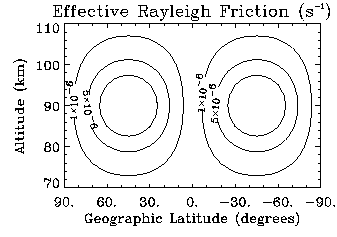
The GSWM
uses an effective Rayleigh friction coefficient in calculations of the
diurnal tide to simulate this interaction (Miyahara and Forbes, 1991). The
figure shows the coefficients under solstice conditions. The coefficients
are reduced to 10% of these values for equinox conditions to represent
weaker interation in spring/fall:
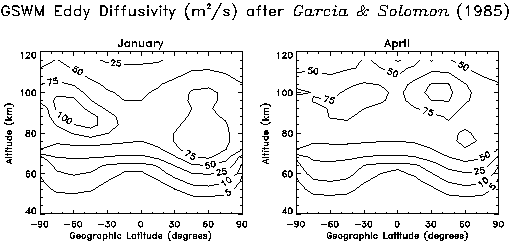
The turbulence caused by these breaking and unstable gravity waves further
hinders the propagation of the tide by diffusing its momentum. This eddy
diffusion is modeled in the GSWM by season-dependent coefficients of
diffusivity that vary by latitude and altitude (Garcia and Solomon, 1985).
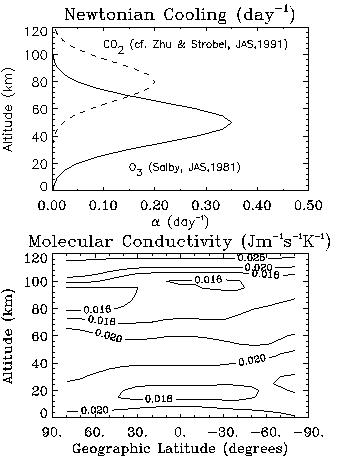
The GSWM also includes parametrizations of damping from heat dissipation (Newtonian Cooling), ion drag from the mechanical acceleration of ions through the Earth's magnetic field, latitude-dependent thermal conductivity, and molecular diffusion of momentum. The figure shows a sample of the Newtonian cooling and thermal conductivity parameters for January investigations.
Back to Top of Model page.
The altitude of each block is indicated at the top of the block by the scale height index, X, and the corresponding geographic height, Z(km). Blocks are printed approximately every 4 km of altitude, beginning at 0km and continuing to 124km, making 31 blocks.
For example,
X= 7.6000 Z= 12.201
LAT= 87.0 U=.278E-02/ 8.5 V=.429E-02/ 5.3 W=.107E-04/ 14.2 T=.681E-03/ 11.1
...
LAT= 63.0 U=.189E-01/ 13.9 V=.188E-01/ 10.9 W=.111E-13/ 12.0 T=.192E-03/ 11.8
LAT= 60.0 U=.199E-01/ 14.0 V=.217E-01/ 11.0 W=.110E-12/ 12.0 T=.397E-03/ 12.0
LAT= 57.0 U=.243E-01/ 13.9 V=.247E-01/ 11.0 W=.435E-13/ 12.0 T=.165E-03/ 8.6
...
LAT=-87.0 U=.706E-02/ 6.4 V=.702E-02/ 10.4 W=.643E-05/ 6.8 T=.278E-03/ 15.7
X= 8.2000 Z= 16.218
LAT= 87.0 U=.188E-01/ 16.1 V=.120E-01/ 0.6 W=.140E-04/ 14.7 T=.115E-02/ 11.6
...
The format in pseudocode and FORTRAN to read each block is:
READ * Skip the line before the block
READ X,Z Read the altitude of this block
FOR LOOP 1 to 59 Read a Line for each of the Latitude values
READ(5x,f5.1,5x,e8.3,1x,f5.1,4x,e8.3,1x,f5.1,4x,e8.3,1x,f5.1,
4x,e8.3,1x,f5.1)
END FOR
READ * Skip the line after the block
There are 4 lines at the top of the file which identify the run, including the month, the period, and the wave number. A positive wave number in the GSWM convention indicates a westward propagating component.
Back to Top of Model page.
Back to Top of Model page.